Coming up with general solutions for Advent of Code is challenging when you only have access to one input. I've attempted to solve this by generating admissible inputs of my own.
The problem
There are two primary problems I'm trying to solve:
-
Many posted solutions claim to be general across all "official" inputs, but, in reality, only work on a subset of those inputs. The authors of these solutions have no way of knowing that their solution isn't, in fact, general, as they normally only have access to one input.
-
Posted performance-oriented solutions are hard to compare because they're often posted with the caveat of "performance on X hardware and Y inputs." While it's possible to normalize for hardware, without access to the inputs it would be difficult to reasonably compare performance, as some inputs are more "difficult" than others.
This is compounded by the previous problem of some of the faster solutions being faster because they were able to take some shortcut that isn't valid for all inputs.
One way to solve this would be to have access to a subset of the official inputs, so that general solutions could be verified as such, and performance-oriented solutions can have their runtime averaged across several inputs.
The problem with this approach is the policy that real inputs should not be distributed nor shared in any way. This policy was previously a general guideline on the subreddit, but, this year, has appeared in the official FAQ.
Rather than debate the ownership and licensing questions regarding the official inputs, I've opted instead to generate admissible unofficial inputs in a way that's free for anyone to use. By "admissible," I mean inputs that should be valid given the inputs I've been able to look at. I've checked the generated inputs against several solutions, mine included, in order to decide if an algorithm generates admissible inputs with a reasonable success rate.
For an input to be admissible, the majority of compared solutions need to agree on an answer, and, for the ones that disagree, I need to demonstrate that the implementation of that solution is actually wrong in order to dismiss the failure.
If you don't care about the assumptions and learnings from this process, the CLI can be found here: https://github.com/mattcl/challengr/tree/master/examples/aoc2023.
There is a repository of 10 generated inputs for every day here: https://github.com/mattcl/unofficial-aoc2023-inputs.
Needless to say, heavy spoilers below. Seeing how I've chosen to generate the inputs will likely give away the solutions to some of the problems.
Contents
- Day 1: Trebuchet
- Day 2: Cube conundrum
- Day 3: Gear ratios
- Day 4: Scratchcards
- Day 5: You give a seed a fertilizer
- Day 6: Wait for it
- Day 7: Camel cards
- Day 8: Haunted wasteland
- Day 9: Mirage maintenance
- Day 10: Pipe maze
- Day 11: Cosmic expansion
- Day 12: Hot springs
- Day 13: Point of incidence
- Day 14: Parabolic reflector dish
- Day 15: Lens library
- Day 16: The floor will be lava
- Day 17: Clumsy crucible
- Day 18: Lavaduct lagoon
- Day 19: Aplenty
- Day 20: Pulse propagation
- Day 21: Step counter
- Day 22: Sand slabs
- Day 23: A long walk
- Day 24: Never tell me the odds
- Day 25: Snowverload
Day 1: Trebuchet
This was pretty straightforward. For this we make a list of keywords we want
included in some strings. These keywords are the strings "one" through
"nine", with the overlaps like "threeight". The real inputs appear to have
manually specified strings, so we include a couple of those, too.
We then generate 1000 to 1100 lines with the following procedure:
-
Generate a string of 1 to 65 alphanumeric characters. Convert to lowercase. Convert any
0characters to1. -
If we're going to insert any keywords into the string (70% probability).
- Pick a number (
N) of keywords to insert between 1 and 6. - Pick
Nindexes from the generated string as our insertion points. - For each point, select a random keyword and insert that keyword into the string at that position.
- Pick a number (
-
If the generated string does not contain any digits, insert a random digit from 1 to 9.
This generates longer lines than show up in the real inputs, but that shouldn't matter that much for general solutions.
Here are a couple of lines:
12ojeoendj9
wthwbtwofl9x8nsevenifft8pbjxsixylvps8kijdiprgooeighthreecjqo7kju3offzdvgcijeninejydj4
ysevenpqvtwooxa5cp6gvk8x3zzsa2m2eightfsevenjplseveninesuagq
5rdeightwow
wtwoneyydesix9
od3otpcthreeicpwnvget4wowu8f5sdcy5ybjxfk9vdwuw1j
pfourcsixmathreeight7
Day 2: Cube conundrum
This is another simple day. The plan is to generate between 100 and 111 games, with each game having between 1 and 6 draws.
We do this as follows:
-
Pick a number of draws.
-
For each draw:
-
Select 3 numbers, each between 0 and 21, ensuring we have at least one number larger than 0.
-
Shuffle the list of colors, pairing one with each of the 3 generated numbers.
-
Construct a string representation of a game, filtering colors with 0 as the selected value.
-
Here are a couple of lines:
Game 66: 11 red, 4 green; 3 red, 10 blue, 18 green; 15 red, 12 green, 13 blue
Game 67: 1 blue, 19 red
Game 68: 6 red, 12 blue, 13 green; 19 blue, 1 red; 10 red, 6 blue, 5 green; 14 blue, 5 red, 19 green
Game 69: 10 green, 7 blue, 15 red
Game 70: 6 blue, 16 green, 16 red; 5 red, 20 blue; 13 blue, 4 green
Game 71: 15 red, 12 blue, 6 green; 16 green, 10 red, 13 blue; 12 blue, 18 red, 13 green; 19 red, 19 blue, 18 green; 13 green, 3 red, 11 blue
Day 3: Gear ratios
The first of the slightly more complicated days. My strategy here was to
randomly select a number of coordinates as the location of symbols, then
randomly arrange numbers around those symbols. While the problem defines gears
as * symbols with exactly two numbers around them, we're going to use gear to
refer to any symbol with up to two numbers around it.
The problem description suggests that there could be many numbers around a given symbol, but, in the real inputs this appears to be capped at 2, so we're going to replicate that. The real inputs also have no symbols on the edges of the grid, so we're going to honor that. Numbers may show up on the edges. Lastly, the real inputs do not appear to have numbers that are next to two or more symbols, so we'll have to constrain ourselves to that.
We're also faced with creating numbers not adjacent to a symbol, so we're going
to cheat by including . as one of the symbols. To create gears around
"nothing".
To "start" the numbers in different locations, we can observe that there are
actually two base configurations (G is the symbol location, S is a starting
location for a number and E is the ending location for a number):
SSS E.S
.G. or EGS
SSS E.S
By picking one of these variants, then picking up to two locations in each "side", we can generate all valid variants, i.e.
.102 .43..
.G.. or ...G.
.3.. 123..
We can insert a gear into the grid, ensuring that no part of it (including the numbers) touch another gear or its numbers. We can do this by maintaining an exclusion grid, where we mark all gear spaces and surrounding spaces as unavailable.
Lastly, we want to encourage symbols to be relatively close to each other, so
what we're going to do is, for every row, R, we will try to place as many
gears as we can starting with a row in R - 1 to R + 1 and a random column in
the row, moving on to the next R after failing to place a gear M times.
The strategy is then:
-
Initialize an empty
N x Ngrid of.chars and anN x Nexclusion grid of boolean values. -
For each row, attempt to insert gears in that row or the one above or below it until we fail to do so
Mtimes:- Generate a gear by picking a location and symbol, then selecting a variant, offsetting the starting/ending locations of the potential surrounding numbers.
- Pick 0, 1, or 2, up to three digit numbers, to place around chosen location.
- Attempt to insert this gear, and, if we succeed, we will exclude all locations around this gear's elements, such that no other gear can touch it directly.
Here's a sample of a portion of a generated grid:
......589..................................824...............265.....................
.....+.......*911.........&...548...........=......368..398....*.....................
.91......................858.....$.....@...580......&......#.87......................
...%............@..............525.......#...............168.............242.785.....
.............568..&..........&.........719......$......+...............$.............
.*......400#.....281...845...../.*...........456.422.473.......%.....................
..249.................@.........................................389.389&.............
..........81..........................464+.....377......635....................#.....
.................+....599....250.............$................+......................
......+.349....................@.....428..542...........$....207.....................
........................%...@.855.......@.........................$......258.........
.............@97....$..................67.......683....=.........204....&............
..........661.................140................$...................677......@....56
.............................$.......391.504....614..=...........138.....+...........
...=...711=.............................+.............734..........$.................
.#.........726....................%...........$...........994.........471......248/89
...&............90...............298.......922.200..........*..199.......#.$.........
You'll note that the real inputs have a denser arrangement of symbols and numbers, but this is good enough for our purposes.
Day 4: Scratchcards
This day appears to be simple enough, but we have to be mindful to prevent inputs that result in solutions that far exceed what could fit in a 64-bit integer value.
Instead of generating cards with a random number of winning numbers, we're going to decide upfront how many winning numbers a card should have, and generate sets of numbers to meet that constraint. We'll restrict the maximum number of winning numbers to 10.
We're going to generate "runs" of winning counts such that we contain the card duplications within the run. Runs start with a card with 10 winning numbers, then end with two cards of 0 winning numbers. A run will consist of 15 to 30 cards. As we near the end of the run, we can limit winning number of those cards such that they do not duplicate any cards beyond the end of the run. For all of the other cards in the run, we can select the winning number randomly. This should prevent the number of duplicates from growing exponentially across the entire set of cards. In testing, this produces solutions that fit within 64-bit unsigned integers.
Generating a particular card consists of selecting 35 unique numbers from 1 to
99 (inclusive). We can then split this into two disjoint sets: one set of 10
numbers for the left side, and one set of 25 numbers for the right side. We then
randomly select N numbers from the right side to replace N numbers in the
left side to construct a card with the desired winning count of N.
In summary:
- Select between 190 and 211 cards as a desired number of cards.
- Until we have enough cards, generate a new run:
- Pick a length of the run from 15 to 30.
- Insert a card with a winning count of 10.
- For the remaining cards in the run, generate a card with a winning count limited by 10 or the number of cards remaining in the run, whichever is smaller.
- Insert two cards with a winning count of 0.
Here's a sample of the generated input:
Card 4: 14 32 19 16 12 54 3 26 75 74 | 14 62 35 60 19 98 26 83 18 74 12 10 75 77 32 16 22 54 24 58 89 88 3 1 63
Card 5: 91 6 27 20 64 18 97 32 62 36 | 4 70 63 17 97 5 3 81 87 38 47 12 30 95 45 42 46 33 82 16 19 89 39 14 96
Card 6: 24 14 20 3 16 47 87 36 46 95 | 63 46 87 42 8 95 17 24 97 36 43 90 92 14 31 4 67 20 57 16 84 3 47 64 39
Card 7: 88 80 73 16 23 91 86 5 17 34 | 33 50 10 24 28 44 95 70 64 56 58 38 15 4 85 91 57 51 88 11 76 31 20 7 46
Card 8: 18 24 44 93 47 32 36 26 31 8 | 52 67 2 28 50 26 24 92 93 31 36 13 47 37 18 11 94 12 8 76 89 71 44 96 32
Card 9: 77 47 60 65 24 9 3 92 88 42 | 38 56 27 66 77 14 10 96 19 1 79 52 81 86 85 78 20 99 87 37 64 98 34 39 23
Card 10: 85 95 67 29 76 24 57 48 86 12 | 4 51 46 88 89 70 20 19 87 92 33 78 28 56 25 39 47 22 95 96 29 42 59 35 45
Card 11: 9 81 72 17 84 77 56 89 76 73 | 56 40 41 84 44 62 54 72 85 25 26 9 63 94 42 89 81 17 76 77 91 55 73 7 45
Day 5: You give a seed a fertilizer
This input consists of two distinct sections: the seed list (which are actually ranges), and the collection of range mappings. The seed list is easy enough to generate:
- Select a starting value between 5 and 6 million.
- Add a random value from 100 to 900 million to this value, repeating the process 9 times until we have 10 distinct values.
- For each value, select a "width" of the range starting at that value where that width is between 50 and 500 million (bounded by the next starting value).
- Construct the seed string using a random order of the (starting, width) pairs, to disguise the fact that they were exclusive and generated in order.
The mapping groups are a little more complicated, but we can ensure that we have exclusive ranges by splitting up the range from 0 to our maximum seed value plus some random additional width.
Once we've split the large range up into 6 to 36 partitions, we can pair each partition with another one of the partitions, creating the source and destination mapping. For each partition, we can then select a width such that we have between 90% and 100% of the values in the partition covered. This should result in "gaps" for the part of the specification that says if we have a value that's not handled, it passes through unaltered.
The real input is generated in such a way that the 0 destination range is not encountered for the location mapping, which prevents the part two answer from simply being 0. We don't know how this actually done, so we're going to cheat and just make there be no 0 destination range for the location map.
So, in summary, for each mapping set:
- Take the overall range and split it into 6 to 36 partitions.
- Shuffle the partitions, then pair each one with another one, creating pairs
of
(source, dist). - Pick a width for each partition that's 90% to 100% of the total width.
- Record these partition groups as
<dest> <source> <width>
Here's a portion of the generated input:
seeds: 1162627782 486594510 2814113085 434809392 4479976160 401655830 4881631990 330229546 411657773 246842407 3248922477 419477195 2044078672 224867951 3668399672 438919608 5839087 355886588 4107319280 217918179
seed-to-soil map:
5166934740 4018727020 554102841
2870519300 0 521227200
2296415440 574103860 542376399
0 4592830880 516851329
574103860 1148207720 561578947
4592830880 2296415440 528119614
3444623160 2870519300 531583530
1148207720 1722311580 556335751
4018727020 5166934740 528936760
1722311580 3444623160 567599405
Day 6: Wait for it
This was relatively simple. We just have to pick four times and velocities and compute their corresponding distances for small enough time values such that resulting distance values are between three and four digits. We can compute this with the equation
(t - v) * v = dist
Once we pick a time t, we know the
velocity is constrained by t, and we can select a velocity from 5 to time - 15. From that value we can calculate dist.
Once we have four of these values, we can validate each of them by attempting to solve the real problem for each pair of time and distance. We can then combine the times into a single value and the distances into a single value (by joining digits), and check if there exists a solution for the joined value. If a solution exists, we have a valid input. If it does not, we can regenerate until we do.
The real inputs are not required to have integer roots for the joined values, so we're not going to constrain ourselves to that either.
In short:
- Pick 4, 2-digit times, from 40 to 99 inclusive.
- For each time, pick a velocity between (5 and time - 15).
- For each time and velocity, compute the distance, recording the time/distance pairs.
- Check that the input is solvable for each time/distance combo, as well as the joined time and distance values.
Here's a generated input:
Time: 49 89 83 94
Distance: 490 1908 1342 1053
Day 7: Camel cards
This was very simple, though the "quality" of the generated hands is maybe questionable in that certain combinations are likely very rare. To compensate, the randomly generated list of hands and bids contains some manually specified hands to ensure we have a five of a kind, etc. To prevent ambiguous ordering, we guarantee that all hands are unique in that the specific order/composition of cards is never repeated.
In short:
- Insert a set of manually specified hands, generating a random bid for each.
- Generate unique hands until we have 1000 total hand/bid combinations.
- Shuffle the hand/bid pairs to break up the manually specified hands.
Here's a sample of the generated input:
Q78KT 898
769T7 214
4Q74Q 286
TQQ87 763
9A9KJ 337
K2A6J 445
JT653 995
633Q4 78
7583A 17
2K6QJ 918
T922K 442
A7989 145
7K85K 16
Day 8: Haunted wasteland
This is one of most "special" inputs in the sense that the problem, as specified is not reasonably solvable in the general sense. The "intended" solution of using LCM requires a very specifically crafted input. This is something I'm not particularly fond of, but it is what it is for this day.
The real inputs I've seen work out such that the part two answer is equal to
K * N1 * N2 * N3 * N4 * N5 * N6, where K, a prime number, is the length of
the left/right instructions, and N1..N6 are six distinct prime numbers that
are the cycle-lengths of six disjoint loops of nodes.
Each loop of nodes has an "entrypoint" node that sits outside of the loop. Each
loop only has a single node that ends in Z, and the entrypoint node is the
only node that ends in A.
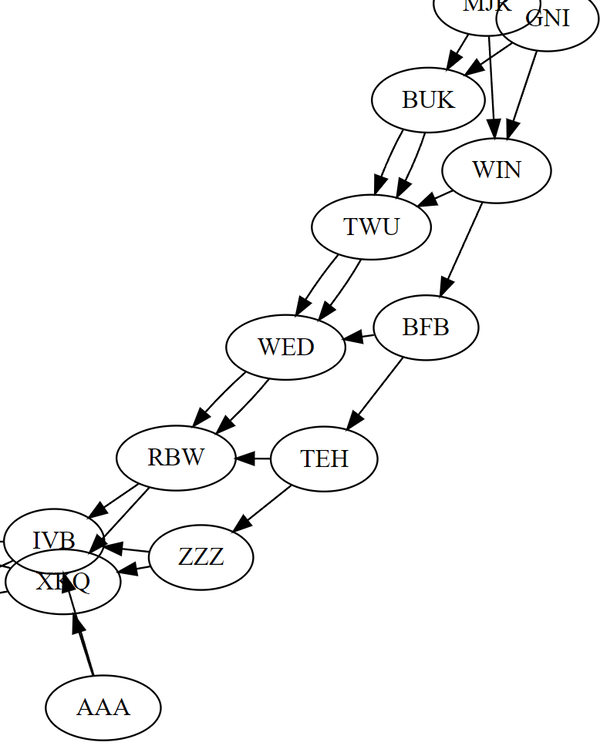
It's simpler to show an example of one of these loops. I've chosen one of my
randomly generated ones that also happens to be the loop with the AAA and
ZZZ nodes for part one:

day 8 loop visualization
We can observe several things. First, the cycle length from the Z-node to the Z-node is the same as the length from the A-node to the Z-node, this is important for the special property that allows all six loops to have their cycles converge. Furthermore, the cycle length for each loop is a prime number.
Second, and importantly, there is a "run" of 3 node-pairs leading up to the
Z-node such that the left-hand nodes have both their left and right pointers
pointing to the next left-hand node. This acts as a shunt around the Z-node such
that, unless you encounter an instruction sequence of RRRR at precisely the
right time, you'll always "miss" the Z-node on your way around the loop.
day 8 loop ending sequence
What this means is that we can generate any sequence of left/right
instructions as long as the sequence RRRR only appears once and at the end of
the instructions.
Putting these special properties together, we ensure that we hit the Z-node in
any loop at exactly step N * K, as long as N and K are prime. This gives
us the property that, for all 6 loops, the step at which all ghosts step on the
end node simultaneously is K * N1 * N2 * N3 * N4 * N5 * N6.
The last component to ensure that this works is that node names must be unique,
and only specific nodes may end with A or Z.
We therefore:
- Select a prime value
Kbetween 211 and 347. - Generate a set of L/R instructions
Kcharacters long, ensuring that we never have a run of 4Rinstructions until the end.- This must start with
Lto avoid wrapping anRsequence around the end. - To disguise the end sequence, we allow 4-length
Lruns and up to 3-lengthRruns to appear.
- This must start with
- Select 6 distinct prime numbers
N1..N6between 23 and 97. - For each number, generate a loop of nodes with a cycle length equal to that
number, then add an entrypoint node that ends in
Asuch that the entrypoint node points at both children of the only node that ends withZ. - For one of the loops, explicitly specify the entrypoint to be
AAAand the end to beZZZfor part one. - Shuffle the generated nodes when writing the input to disguise the separate loops.
Here's a portion of some generated input (newlines added for display):
LLLLRRLLLRRRLLLLRRLLRRLLLLRRLLLLRRLLRLLLLRRLLLLRRRLLLLRRRLLRRLLLRRRLLLLRLLLLRRL
RLLRRRLLRRRLLRRLLRRLLLRLLLLRLLRRRLLRRRLRRLLLRRRLRRLRLLRRRLLLRRRLLLLRLRRRLLLLRLL
LLRRRLLLLRRRLLLRRLLLLRRRLRRRLLLLRLRRRLLRRRLLRLRLLRRRR
VIR = (VKM, GDY)
HWE = (EDN, MCX)
LWJ = (XYS, UWK)
OGU = (IND, USJ)
FFV = (WHM, RFW)
WEQ = (HOM, RVJ)
XTW = (QLC, WER)
XHD = (BNX, XEX)
Day 9: Mirage maintenance
This day is one where my generator may produce inputs that have a negative part two solution. While this is not invalid by problem specification, it may be considered invalid as far as "real" inputs go. It would probably be simple to check for this and regenerate, but I didn't bother.
The strategy is simply to pick a starting "depth" from 1 to 19 for which we will create a "row" of all zeros.
depth 3: 0 0 0
From here, we can compute the remaining rows up to a depth of 21 by selecting a starting value for the next row between -5 and 15, and computing remaining values in that row using the previous rows values as differences.
- Pick a "depth" from 1 to 19
- Create a depth-wide row of all zeros.
- For reach row from the current depth up to 21, select a starting value from -5 to 15, then compute the remaining values in the current row using the values of the previous row as differences.
Here are some rows from the generated input:
12 16 17 13 8 25 114 352 832 1638 2803 4247 5692 6551 5788 1746 -8060 -27188 -60555 -114767 -198496
14 22 43 72 102 129 170 305 752 1982 4875 10904 22308 42173 74278 122477 189274 273102 363635 434240 430410
7 4 13 39 93 204 433 902 1848 3720 7365 14401 27947 53957 103458 195975 364273 660168 1160441 1970687 3223069
-1 -6 2 30 94 223 463 881 1569 2648 4272 6632 9960 14533 20677 28771 39251 52614 69422 90306 115970
13 11 17 42 97 193 341 552 837 1207 1673 2246 2937 3757 4717 5828 7101 8547 10177 12002 14033
5 17 29 41 53 65 77 89 101 113 125 137 149 161 173 185 197 209 221 233 245
2 12 35 78 155 298 576 1132 2248 4448 8649 16370 30009 53198 91246 151680 244894 384916 590303 885174 1300391
0 3 18 55 138 305 608 1113 1900 3063 4710 6963 9958 13845 18788 24965 32568 41803 52890 66063 81570
1 -2 -5 -8 -11 -14 -17 -20 -23 -26 -29 -32 -35 -38 -41 -44 -47 -50 -53 -56 -59
7 20 35 55 80 108 145 223 435 1017 2534 6258 14871 33716 73015 151875 305659 599614 1153793 2187629 4097446
Day 10: Pipe maze
One of the trickier days because we have to generate a closed path that has certain properties. If we look at the real input, we notice that the path is quite dense, and the number of enclosed non-path cells is quite low. This is probably a byproduct of the algorithm used to generate the path, so we're going to attempt to replicate the overall "texture" of the path.
To do this, we'll start by forming a rectangle comprised of points around the center of our grid. By starting with a closed path and altering it in ways that do not break the path, we can ensure we have an arbitrarily complex loop. We can alter this by attempting to insert 2 new points between any existing pair of adjacent points. The 2 points we insert will randomly be above or below or to the left or right of the original pair of points.
x-x x-x x-x
| | | | | |
x-x-x-x-x-x x-x-x x-x-x x-x-x x-x-x x-x-x x-x-x
| | | | | | | |
x x -> x x -> x x-x x -> x x-x x-x
| | | | | | | | | | | |
x-x-x-x-x-x x-x-x-x-x-x x-x x-x-x-x x-x x-x-x-x-x
We can use a set to track the locations that are already part of the loop so we don't overlap ourselves.
By repeating this process until we've filled enough of the grid, we can come up with a dense, closed path similar the ones in the real inputs. To guarantee that there's an enclosed area in the middle (like with the real inputs), prior to altering the initial rectangle, we can mark arbitrary clusters of points inside the rectangle as having been "seen," which will prevent our algorithm from filling those locations in. Since they're inside the loop, we know we'll at least have that much area contained.
This loop growing algorithm will be used two more times on day 18 and day 23.
To summarize:
- Initialize an empty grid.
- Generate a rectangle of points in the center of the grid.
- Randomly mark locations inside of the rectangle as "seen" for our growing algorithm (ensuring we have an enclosed area).
- Repeatedly alter the rectangle by inserting points until we've filled a large portion of the grid.
- Iterating around the list of points, place the correct symbols into the grid.
- Replace a random point on the loop with the
Sfor the starting location. - Randomly replace the remaining cells in the grid with random symbols to hide the loop.
Here's a portion of the generated input:
||77|.7L-|J7..J7.|7L-LF.7LLJ||.77|7-77.F|.F..F|F..-|-.F-7J|-.F7FF.F7F--7FJ..LL.-||..7-LF..F--
.7-F|7F777-J7|-.LFFL-.|---JF..77F7F.L|.JFL..|L-7-FF7LFL7L7F7FJ|F7FJLJF-JF7F-7-.7--..7FJ-.|L-7
.FJF.|L|J7FJJJ-.7J7LLL|F--J|-FFLJ.J7777.J7FL7J7.F-J|7F7|FJ|LJFJ||L--7L7FJ||FJ|..F-|J..-L||-FJ
J..---LF|LF--FLF.FJF.7L.-|7.|..J..L.--J.--.F...LL-7|FJ||L7L-7L7||F7FJFJL7LJL7....L|J-|LFL|FJF
.J77|.|FJ.LJJJ|F7L7J..F-L7F.FF-J|F77.|LJL7J7L.JF-7||L7|L7|F7L7|||||L7L-7|F-7L7LFF7FF.--LF7L7|
||.F.JF7F-|J7L.J|-L7-|J-J.J.LFFJ..L77L...7-.J.LL7LJL-JL-JLJ|FJ||||L7|F-J|L7L-JF7||J-.JLFJL-JL
FFF.J.|JJ7J.F7.F-.7LL-.-J|..J.J-FF.FJ..LLF-7F7F7L------7F--JL7|||L7|||F7|FJF7L||||.JJ|.L---7F
J77|JFFF.||.-|FJ7.--.LL..7-L.FLJ7.LF7..LFL7||||L-7F----JL-7F7|||L7|||LJ||L7|L7|LJL7F.F--7F7||
|7-...|.L77-J.-J-..7-..LFLLL-F.L.|FJ|F7-F7||||L-7|L----7F-J|LJ|L7||||F-J|FJ|FJL-7FJF7L-7LJLJL
F..F7F.|F.L7|.LL--777-7LF||7.|-77LL7|||FJ|||||-FJL7F---JL-7L-7L-J||||L-7||.|L-7FJL7|L77L--7F-
L|L-J.F7LF.L7|LF...-|...FLJ.-||.F7-||||L7|||||FJF-JL---7F7|F7L--7||||F-J||FJF-JL7FJ|FJF-7.||F
-LL.J-J..L-|L|JFJJ.-F|..|..L....||F||||FJ|||||L7|F7F7F-J|LJ|L---J||LJL--J|L7|F-7|L7|L7L7|FJ||
.FFJLFJ..J.77-FL-.LJL|J-L|F.L7F-J|FJ|||L7|||||FJ|||||L-7L7FL--7F7LJF-----JFJLJFJ|FJ|FJ|||L7LJ
F-J|FFL-J7-7.-|7FJ||-.......--L-7|L7|||FJLJLJLJFJ|||L-7L7L7F7JLJL-7L-7F7F7L7F-JFJL7|L7FJL-JF-
7L-7L|-JLJ-.JLF-..7JL.FJF....F.FJL-JLJ|L-----7FJFJ|L7FJFJFJ||F7FF-JF-J|LJL7||F7|F7||FJL---7L7
LF7LLF.-L-.FL.|JJFF-L7F7..7J..FL-----7L------J|FJFJ||L7L7|FJLJL7L-7|F7|F--J||||||LJ||F7F7FJFJ
.-FJJF7.-|F-FJ--J..J.F||JF-7F7F7F7F--JF------7|L7L-7L7|FJ||F---JF-JLJLJ|F7FJLJ||L7FJ|||||L7L-
LFJ|L|J7...|.JLJF-LF-FJ|FJFJ|||LJ|L---JF7F7F-JL7|F-JFJ|L7|||7F-7L--7F--J|||F--J|FJL7|||||FJF-
.-..||-.-.F|LF..|.|FJL7|L7L7||L-7|.F-7FJ|||L--7LJL7FL7|FJLJL7L7|F7FJ|-F7||||F7FJL-7||||||L7L7
Day 11: Cosmic expansion
This day was very simple:
- Create a 140x140 grid of
.characters. - Select 400-450 random locations in this grid to set as
#, re-picking if a selected location is touching an existing#.
The real inputs appear to exclude 2 around an #, but excluding just immediate
neighbors still meets the problem definition.
Here's a sample:
....................................................#..#....................................................#...............................
............................................................................................................................................
...............#..#.........................................................................................................................
...............................................................................................................#............................
..................#...............#....................................................#....................................................
........................#................#..................................................................................................
.....#.....#.......................................................#..............#....#..........................#......#..................
..................#..................................................................................................................#......
.....................................................................#......................................................................
..................................................#...............................................#....#....................................
............................................................#............#..................................................................
....................#..................#.........................................................................#........................#.
......................................................#........................#..................#.........................................
.....#..............#.......#.....#.........#................#........................#...#.................................................
...........................................................#.....................#..........................................................
....................#...................#...............#....................................................................#..#...........
..................................#......................................................................................#..................
Day 12: Hot springs
My initial guess examining my input would suggest that many of the input lines
were hand-crafted to guarantee that certain examples showed up. Instead of
trying to replicate that, I'm taking the approach of simply generating a random
set of groups, then creating the strings that could satisfy those groups. By
further connecting those strings with either . or ? chars, we can introduce
variance into the groups to allow for more potential solutions.
- Generate one or more single-digits to use as the groups.
- Generate a string that satisfies each group with a random selection of
#and?characters. - Join the groups by a random small number of
.or?chars. - Repeat N times until we have enough lines in the input.
The actual quality of these randomly generated inputs is rather poor:
??#???.??#?.????..??#?? 5,3,4,3,1
#?#?? 5
?##??.##???. 5,5
#??#.?? 4
#??#??##.?#? 4,2,3
#???.#?#### 3,6
#?#?.??...#???? 4,2,2
#.?. 1
?#####.???#. 6,2
?#?.????.??##??..???? 3,1,5,1
???????#??###.#??? 1,3,6,1,2
?#?##.??##..?##.?.?#?# 5,1,2,2,4
???????.##????..???...##?#? 6,5,3,5
?#?#.??#### 4,5
#?#?.???#.###.?###..???##.? 3,4,3,3,4
?#..#####?..#?..#??.### 2,5,2,3,3
#?#??.. 4
#?##??.?#?? 5,3
###???##?#?.?.? 4,3,1,1
#??????#??.?#?####???..###?#? 4,5,2,6,6
Day 13: Point of incidence
These inputs are constrained enough that, looking at my real input, it would appear that there were a pre-generated selection of mirrors that were then probably randomly flipped/rotated to produce distinct inputs/solutions. Many of the mirrors in the real input have an almost-symmetric section with two symmetric rows slapped on an edge. We should be able to randomly generate those kind of mirrors.
The plan is to:
- Pick a random mirror size between 10x10 and 20x20.
- Pick a random row to begin the part 2 symmetry.
- Generate a random row of
.and#chars. - Insert this row such that it's symmetric across the chosen location.
- Repeat, moving outwards from the chosen location until the mirror is filled.
- Change 1 random location in the symmetry region (for the smudge).
- Append 2 symmetric rows to the side of the mirror furthest from the line of symmetry (for part 1 solution).
- With a 50% chance, rotate the mirror 90 degrees.
- Using the logic for the day 13 solution, verify that the generated mirror has a unique part 1 and part 2 solution, rejecting the mirror if it fails this constraint.
- Repeat until we have 100 mirrors.
Here are a few mirrors from the generated input:
.#..##..#.#..
#.#.##.#.#.##
..######...##
#........#.##
.#.#..#.#.###
.#.#..#.#....
.#.#..#.#....
##.#..#.##...
.##.##..#.###
..######..#..
...####...#..
##..##..#####
..#.##.#.....
#..####..####
#....####....##..
#.##..##..##.#...
....#.##.#.....##
....#....#....#..
...#.####.#....##
.#..##..##..#....
.###.####.###..##
#.#.#...##.#.##..
#...#....#...#.##
..#.#....#.#.....
###..##.#.
###..##.#.
.#.#.#.#..
.#.#.##.##
...#.#..#.
.###..#.#.
#######...
#.##.##...
#.##.##...
#####.#...
.###..#.#.
...#.#..#.
.#.#.##.##
Day 14: Parabolic reflector dish
This day was surprisingly "simple." Originally, I had thought that I'd need many attempts to find an input that had a cycle start and period that were "nice" enough to be solved by most people in a short amount of time. It's been shown elsewhere that it's possible to devise inputs with enormous cycles, so I was worried I'd have a low success rate generating "nice" inputs.
In reality, the density of rocks (round and square) likely means that a cycle occurring after a small number of iterations is very likely. It's also probably the case that the period of the cycle is also small.
The strategy then becomes:
- Generate a random 100x100 grid of
Oand#rocks.- Generate between 1600 and 1700
#rocks. - Generate between 1900 and 2100
Orocks.
- Generate between 1600 and 1700
- Run the resulting grid through my solver for day 14, limiting the number of tilting iterations to under 400.
- If the cycle is not detected and contained in 400 iterations, repeat from step 1 up to 5000 times.
- If we haven't found a nice input after 5000 attempts, return an error.
- Otherwise, return the generated input.
Thankfully, my day 14 solution executes in 2 ms, so checking the full input on every attempt should still produce inputs in a reasonable amount of time.
In practice, this approach produces valid inputs after the first attempt, so 5000 attempts should practically guarantee a solution.
Here's a portion of a generated input:
.O#.........O..O..O.O....###..###.#.#..#.......#O....#...##....#.O..##...#..O..O#O...#...O..#.......
O.#.##..O.#........##O.##....#OOO....O####....#O#....#.#.#O#O..O...O.O.OO..OO.O#.....O....#O..##OO.O
##...O....OOO..#...O#..O......#O...##..#O.O.O.O#.#.O....O......O.#..O..O....O..O.#.O.#...O...#O#O.#.
.....O.......#OO...O...OO.O.O##......#..O.OO....#...O.#...#..O....#..#O...O.....##O.O....#...#...#O.
.#..OO#.OOO#O.#.#O...##.O#.....#..O#..........#..#...#.....#..#.......O.##.OOO#..OO..##.#.#..##.OOOO
..O.....##.#....##........##......O.........O.#....O...#O..OO....O#...OOOO#....#.OO.O#O...O.O#O.....
.##.O...O....##.O......#O#..#..O#.O#.O..OOO..O....##..#....#OO#...#...O.O.#.....O...##....OO#.O...O.
...#..OO.O.#.......#...O........#...O....OO........O.#O.#.#...##.#OO.....#.O#O..#....O#O...OOO..O..O
##O#..#.#...#....OO.O..O#O##OOO.O..O...O....O..#.O.O....O.OO..#O#..O...#..O..##.....O....#O....OO.#.
O....##.OO.........O...O.O..O..O.O.#O.#O.O.#..#.....#.##O#....#.##.....O##.O.O..#..O.##..O...##O..#O
....O..#.#..O...OOOO..OO........#O#.#..O......O.#..#OO..O.O...O#.#..#..O...........#.#OO....#....#O#
.OO.....#.......#.....O..O#O.....O.O..##..#..O...#O.#O...#.....O.##OO#..#..OO......O..#...OO.....##.
O......O...#.#.#.OO#.........O.O.O..O#.O...#.O....O.#O.#O.OO.O..O...#O.O.O....OO.O#......#.O.O...O..
O...O...O#...O....O.O..OOO..OO#.#......#.#..O.#....#O.OO..OO.#.OO....OO#OO.O.#..O...............#.O#
..#O.O....O...#OO...O....#....##.........OOO.#...#O...O........O.OO....#....#.#.##......#.#O..O.O...
...#.O.....O.#..O..OO.O....O.O..O.O..OO...OOO.#O#....O.....#.....#...........OOO.....#O#.###...O.#.#
Day 15: Lens library
This was relatively simple:
- Generate 500 to 600 unique keys of 2 to 6 characters.
- Generate 4000 to 5000 key/operation pairs using the pool of keys.
- For add operations, select a random value from 1 to 9 as the inserted lens.
- Join these key/operation pairs into a single line by separating them with commas.
Here's a sample of the input (newlines added for display purposes):
ibvg-,iyp=6,ffk-,tpdes-,iswjvp-,pd-,synida=9,gusue-,hccq=5,pz-,wxqnk-,rdomr-,
tpb-,pmk-,rvz=3,wrs=9,zn=4,yiqjk=9,ulqfb-,hwdthz-,salccs-,pnhjr-,sw=4,tzeph=2,
cgdwwk-,dmvovm=2,tzeph-,tzeph=7,sz=5,jzhk=4,nixn-,pseme=2,ecpw-,eguy-,hikynr=7,
cffz=2,stmb-,pgkmi-,ahjwds-,vwpxbx-,ood=7,qwmm=1,fv=4,gt=8,xz-,ohvll=6,pnmodp-,
nlm-,ood-,yxje-,pseme=4,wfrugn=3,sju=5,mjou-,udsklf-,fzv-,tfhfac=4,tn=5,ecyl-,
bkccgw=1,qykjb-,slv-,tywj-,epwdv-,gdnvfo=9,sirsr-,hnpkv-,haqi=7,ishaky-,ej-,
ke=6,ry=9,sbnvym-,hclje-,wt=7,auj=5,fbnrc=2,btd-,qm=2,scfi-,ekqtc=6,wa-,
pxznxw=6,lcgb-,yiqjk-,uzbdf=7,ga=8,udk-,qzroui=6,qga-,ewev=3,ykx=4,rcdr-,tt=5,
pseme-,wmrnj=5,ukf-,rhdk-,bybhux=4,jkvzsr=6,sbnvym=4
Day 16: The floor will be lava
There is a high variance in the "quality" of the inputs we generate for this day, in the sense that the part one solutions may be very small. A more robust approach may be to ensure loops exist for part one, but this could be a later extension.
The generation process is simple otherwise:
- Generate a 110x110 grid of
.chars. - Select 1100 to 1300 random locations in the grid to insert one of the four symbols.
- Ensure that the top left corner contains
\.
Here's a portion of the generated input:
\...........|.........\............-................|..............\.|-...\.......\.............../.../.../...
.........-..........-.|......./...\....../.-.........\.\......|..........-....-../........................|...
..\.............../......................../../\...../|./.............|....\...................../.\......-...
....-./-........................-.............................|................................\/.-...........
...|...............|.....................\....................|......................\........................
......../........................|........../.....................-........../.....\........./................
|..../..................|...\...\..................|..../-.............|..........................|\.-........
....|...|...\|.....|.....\.....-....................................-.........../.\....................../....
.................................\.|................................\.........................|..|../.....-...
....\....\...../............./........|.|...................-........|.......\.\..-.............../...\./....|
....-..../......|/......\.\..\...........||........................|.-....|/..............././-././.....|../..
..........\.....-..............|................|...-.....\.................|......\............./......../...
...\..../.............\.........\...............|.........|...--.........-........................|..-........
............-....|.......\..../...|.......-..-|..-...../.../...................................../....-..\....
.....|......|.................................../........|........../................./...-./............-...\
...-................\...............-..|-...|.............|...............|......................\...|........
Day 17: Clumsy crucible
The generation for this day is also pretty simple. The real inputs have a "mound" in the center of the grid that contains higher values than the surrounding locations. We can replicate this by using a different random distribution for the cells within a certain distance from the center of the grid.
- Initialize a 141x141 grid of digits.
- For each cell
- If the cell is within
141 / 2 - 6steps from the center, pick a random digit from 4 to 9. - Otherwise, pick a random digit from 1 to 7.
- If the cell is within
Here's a portion of the input:
131145426664234143556113251662644113246246636552356436411424612225134653212661
413636422612542566312151121525245113224162346643123156241411613441245653331465
142552656221332141263526636622611255134553313141223355411225332332615156446334
161165543242462154144256155522326525211646541251442346143546561316145125342361
361446621343152524334246333454256655416541344452211432336551636525163243245262
552542436365113525356345142533455564356434243142333563664642664264133421116252
414254331631254236316522256544325366441412353641416333124616664655562332612513
551631424426221432254212565332456466422342244321344113633164316355134656323323
433511161321556665446622566544623216235525551453322653353146455616231555241326
144344442242456426151353456641333641364426253251434564233463241241266795621325
266531516313261235652352644565116622466561455155531661111152664642146449783434
451126664235314646634426315345134111322524353525621534124236346535794445449451
624241513242564562564214214324625641225515664344431351244353111336557957489856
Day 18: Lavaduct lagoon
For this, we're going to use the same approach to generating the loop for day 10 to generate two separate loops for part 1 and part 2 that have the same length. We're then going to "condense" the loops by attempting to remove points that are not corners, so that we don't have a lot of repeated adjacent directions in the input. We will then randomly scale each loop with a different factor for x and y. The factors for part 2 will be much larger.
In short:
- Generate a large rectangle in the x/y plane, with the lower left corner at (0, 0).
- Alter this loop by randomly inserting additional points between every pair of points.
- Repeat the alterations N times.
- Generate a second loop using the same procedure, stopping only when it has the same number of points as the first loop.
- Condense the loops by attempting to remove all points that are not corners.
- We attempt to remove a single point from each loop, stopping the process if one loop can no longer be shrunk. This ensures both loops still have the same number of points.
- Scale each loop in the x and y directions, picking very large scaling factors for the second loop.
- Write the movement instructions as distance between the remaining points and the relative locations of adjacent points.
Here's a sample of the input:
L 2 (#0657e3)
D 9 (#04ccd2)
L 2 (#0657e1)
D 24 (#04ccd2)
L 2 (#0657e3)
U 3 (#04ccd2)
L 2 (#0657e3)
U 3 (#04ccd2)
R 2 (#0cafc1)
U 3 (#04ccd2)
L 2 (#0657e3)
U 3 (#04ccd2)
R 2 (#195f81)
U 9 (#0e6672)
L 2 (#0657e3)
D 6 (#0999a0)
L 2 (#0657e3)
D 6 (#04ccd2)
L 2 (#0657e3)
U 6 (#04ccd0)
L 2 (#0657e3)
D 3 (#0999a2)
L 2 (#0cafc1)
Day 19: Aplenty
The generation strategy for this day is relatively simple. The real tedium was in implementing it. It's another range splitting problem like day 5.
- Generate random node keys into several "layers".
- For each node in each layer, randomly select a rule, attribute, and value
targeting a node in the next layer.
- For the last layer, all target nodes are either "Accept" or "Reject."
- Repeat until each node has at least two rules in the workflow.
- Randomly generate N inputs for the workflows.
- Randomize the order of the previously generated nodes for output to hide the tree ordering.
Here's a sample of input:
ecf{s<1067:R,R}
ij{s<2094:ni,uol}
urs{m>2392:R,R}
ogo{s<2439:R,s<2638:A,R}
sw{a<1117:tab,m<2273:zyq,uh}
rqv{m>1294:bg,a<1474:pjj,x>1395:sw,s<1311:pqa,gp}
zij{s>2539:A,A}
nl{x<2471:tz,s>2627:xma,m<2524:rkm,wzf}
qks{x>1576:A,A}
wh{x>2805:uad,wid}
cet{m<2715:upa,a<2230:qwj,m>1623:wr,x>2392:xog,ef}
vc{x>2217:R,R}
phk{s>1525:A,a>1523:R,A}
em{a>1213:zbk,xu}
bem{s>2149:R,a<1313:A,A}
yex{x<2948:A,A}
fe{s>2012:R,R}
{x=51,m=388,a=1563,s=2386}
{x=3524,m=2830,a=3755,s=1946}
{x=3356,m=1232,a=3315,s=3705}
{x=3788,m=2079,a=2224,s=1814}
{x=3188,m=948,a=34,s=807}
{x=3267,m=2807,a=347,s=3560}
{x=3625,m=1376,a=216,s=3527}
{x=698,m=1308,a=2324,s=1326}
{x=520,m=3529,a=2040,s=2021}
{x=828,m=373,a=3439,s=1006}
{x=1559,m=2704,a=3191,s=1128}
{x=1548,m=1855,a=3382,s=1257}
Day 20: Pulse propagation
This is another example of a problem that is extremely nontrivial to solve in
the general case, but doable because the input is very special. Essentially,
chains of 12 flip-flops form 4 binary counters, and they're each wired to a
conjunction such that when a specific set of "bits" are 1, the conjunction
receives all high pulses and emits a low pulse. The low pulse has the effect of
resetting the binary counter as well. The final node only receives a low pulse
if all four counters emit their low pulses at the same time. To make the problem
simpler to solve, the real inputs select 4, distinct, 12-bit prime numbers for
the counter values tied to the low pulses. This results in a part 2 solution as
the simple product of these prime numbers.
Generating this input is simple, but tedious.
-
Select 4 12-bit prime numbers.
-
For each prime, construct a set of components consisting of 12 flip-flops and 2 conjunctions, wiring the inputs to the first conjunction as the outputs of the bits corresponding to the 12-bit prime. Wire the second conjunction as the only output of the first conjunction (to act as a NAND gate).
- For every flip-flop bit that's not part of the prime number, configure the conjunction to send a pulse to that bit.
- The 1-bit always has a pulse coming from the conjunction.
-
Wire the NAND conjunctions of each prime group to the final conjunction.
-
Write all of the component descriptions to the input, randomizing their order.
Here's a full input for day 20:
%ec -> hf
%gs -> np
%bp -> lg, os
%oa -> af
&jc -> rx
%ub -> iq
%hg -> lg, yn
%jb -> cg
%jx -> cm
&lf -> sp, ec, hf, nr, sh, ay, gs, np, xj
&lb -> jc
%cm -> dk
%tl -> jb
%xk -> xl
%os -> lg, mi
%kh -> sc, yf
&vx -> jc
%lp -> vw
%yn -> ol
&ty -> jc
%iq -> cg, tl
%np -> mp
%db -> sc, hu
%ea -> lf, gs
%dk -> xi
%an -> lf, sh
%ji -> lg, qi
%vw -> oa
%hf -> an
%uk -> lf
%sb -> ei
&lg -> ji, qi, yn, vx, ol, bs, nc
%mz -> cg, xk
%yq -> lg, bp
%um -> cg, ie
&sc -> db, hu, lp, vw, oa, jx, cm, ty, dk
%mi -> lg
%hu -> lp
%yf -> sc
%xi -> sc, kh
%gj -> lg, hg
%ol -> bs
%sp -> lf, ec
broadcaster -> sp, mz, ji, db
%ay -> ea
%ei -> cg, ub
%yg -> um
%bs -> nc
%xj -> uk
&cg -> mz, xk, yg, sb, ub, lb, tl
%ie -> cg, sb
&nr -> jc
%sh -> ay
%qi -> gj
%af -> sc, jx
%nc -> yq
%xl -> cg, yg
%mp -> lf, xj
Day 21: Step Counter
This was another day where examining the input was necessary to solve the problem. It's also one of the days where it would have been beneficial for people to have access to multiple full inputs. Many of the "general" solutions took shortcuts that fail to solve all inputs. In fact, one of the fastest solutions out there fails to solve most real inputs.
These inputs must be 131x131, with a starting location at (65, 65), Furthermore, there can be no "walls" in row 65 or column 65, and no walls around the edges.
The real inputs also have a diamond void around the center, which is not strictly necessary, but we can replicate it by avoiding placing walls in locations that are within a manhattan distance of 65 +/- 4 from the center.
In short:
- Initialize a grid of 131x131
.chars, setting aSat position (65, 65). - Generate 1800 to 2400 random locations where:
- Locations are not along the edges.
- Locations are not in the 65th row or 65th column.
- Locations are not with 65 +/- 4 steps via manhattan distance from the center.
Here's a portion of the generated input:
...................................................................................................................................
......#.......#...#.......#.......#.............#.........#............#.#...........#..#.............#......#..............#......
...........##.......#..#............##...#.......#...#...#......................#.#.....#......#............#.##............#......
.................#..#.....#.........#....##........#............................#....#..#.......#...##.#..#......##................
...##.#..#...#...#.....###.......##...........#....#..##....................................#..........##.#..##.......#.....#......
......................##......###..#.................#..#.....................#.............#.................#....................
..........#..#..##..#.................#.....#.....###...........#..........#.....#....#....#...##...#....#.#.........#..#....#.#...
.#..#....#....#.#......................#....#......................#.........###......#..##..#..##..................##.#.#.#....#..
...................##.#....##................###.#..................#................#.....#.....#.#...##..#..#....#.........#.....
.....#....#...........#.....#.##....###.#....#..#..#................#...................#...#........#.#......#.#..........#.......
..#..#....#...#......#..........#...#..#....#...................#......#...........#.....#..#.#......................#..#....#.....
......#...................#..#......#.......##..............#.#.......#.................##.#....#..#.....##......#..#..#.....#...#.
.#........#......#....#..##..........#...#....#..........................#............##..............................##..#..#...#.
...#...#...#...................#..............#..........#..........##............##........................##.#..#.#..............
.............#..............#.....##..#..#......................#........#.........#...#.#.........#....#...................#......
...##......#............#................#..........................#....................##..#...#........#.....##.....##......#...
................#...#...#......#.......#..#..#..........##............................##...........#........#..#.##.............#..
...........#...#.................#..#........................#....##......#.....................#.........#..#.....#...#...#.....#.
Day 22: Sand slabs
This day is relatively simple, but we're going to increase the probability of having slabs stack onto each other by biasing our selection to start at a particular edge for a given orientation.
We're going to bias ourselves toward generating horizontal slabs over vertical ones.
- Generate 1250 to 1300 slabs by
- Selecting a random x and y between 1 and 9.
- Selecting a random z between 1 and 300.
- With a 95% chance, project the slab 1 to 9 units along the x or y axis.
- With a 5% chance, make a vertical slab.
- Reject slabs that intersect an existing slab, regenerating as necessary.
Here's a portion of the generated input:
1,6,98~8,6,98
1,4,143~2,4,143
4,0,149~7,0,149
4,8,68~6,8,68
3,9,139~5,9,139
2,0,90~2,0,90
0,2,48~0,9,48
2,1,140~2,3,140
2,6,88~4,6,88
4,2,164~4,4,164
3,2,101~6,2,101
3,2,84~8,2,84
2,7,180~3,7,180
0,1,226~0,3,226
0,3,38~0,5,38
0,0,263~0,0,263
0,8,181~4,8,181
8,0,204~8,2,204
6,1,61~6,4,61
6,3,40~6,3,40
3,5,126~7,5,126
6,3,219~6,4,219
Day 23: A long walk
This was the hardest input to generate (for me, at least). The only purpose of the input having the appearance it does is to obfuscate what the actual problem is. We could just generate a very simple graph connecting 36 nodes together and make a "valid" input, but where's the fun in that?
First, an observation: if we reduce the input maze to just the junctions, we get a representation like the following:
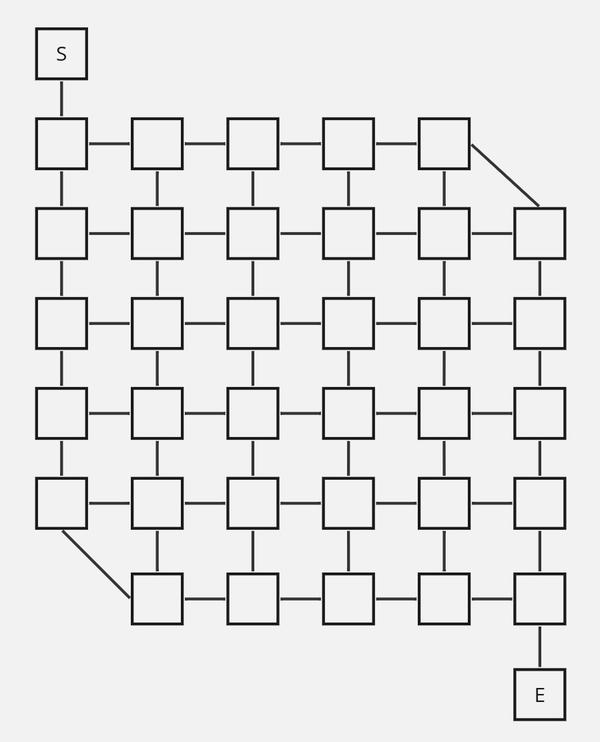
day 23 condensed
Using this, we can approach the problem by dividing the maze grid into 36 "tiles," each containing one junction. The upper right and lower left corners are special, in that the junction we create in them will only have two neighbors, but it's simpler to treat them as full junctions. In the following image, the black dots are the randomly selected junction locations.
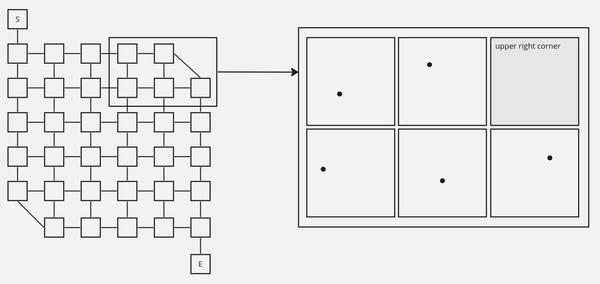
day 23 tiled grid
From this point, we can form lines between each junction and its cardinal neighbors. This can be done by just taking the shortest path between them that does not cross any other line. Once we have these lines, we can apply the alteration algorithm from Day 10 to distort the lines into the paths we see in the final maze:
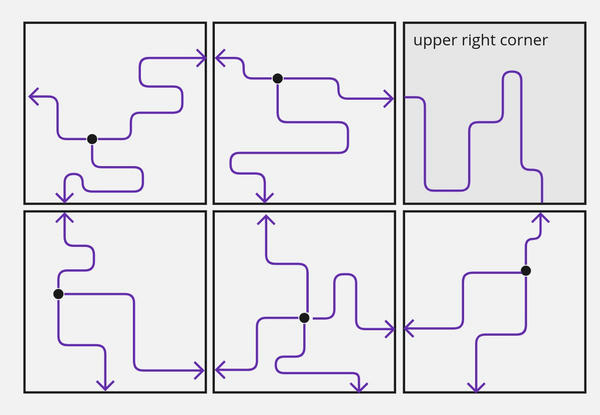
day 23 connecting the junctions
This produces mazes that look similar to the real inputs, but there are clear
biases in my generation algorithm in which a portion of the upper row is not
entirely filled in. It doesn't matter for the solving of the inputs, but it is a
visual feature. This was an off-by-one error restricting the path mutations,
and is fixed now.
For part 1, we can, at every junction, insert arrows pointing toward the lower right corner to prevent you from walking back "up" away from that corner.
Summary:
- Divide the space into 36 tiles, placing a junction at a random location in each tile.
- Connect each junction with the junctions in the (cardinal) neighboring tiles
using a line of points.
- Add special connections for the start and goal.
- Alter each line of points by attempting to insert two new points between every pair of points.
- Repeat until the grid is filled.
- When rendering the grid, render arrows pointing toward the lower right corner at every entrance and exit from a junction.
Part of the maze:
#.##############################################################################################
#...#...#...#####...#...#.....#...#...#...#.....#.....#...............#.......###...#...#.......
###.#.#.#.#.#####.#.#.#.#.###.#.#.#.#.#.#.#.###.#.###.#.#############.#.#####.###.#.#.#.#.#####.
###...#...#...#...#...#.#.#...#.#.#.#.#.#.#...#.#.#...#.............#.#.....#...#.#...#.#...#...
#############.#.#######.#.#.###.#.#.#.#.#.###.#.#.#.###############.#.#####.###.#.#####.###.#.##
#.............#...#.....#.#...#.#...#.#.#.....#.#.#.......#...#.....#.#...#.#...#...#...#...#.#.
#.###############.#.#####.###.#.#####.#.#######.#.#######.#.#.#.#####.#.#.#.#.#####.#.###.###.#.
#.#.......#...###.#.#...#.#...#.....#.#...#.....#.#.......#.#.#.....#.#.#.#.#.#####.#.#...#...#.
#.#.#####.#.#.###.#.#.#.#.#.#######.#.###.#.#####.#.#######.#.#####.#.#.#.#.#.#####.#.#.###.###.
#.#.#.....#.#.#...#.#.#.#.#.#.>.>.#.#.#...#.#.....#.#.>.>.#.#...#...#.#.#.#.#.>.>.#.#.#...#.###.
#.#.#.#####.#.#.###.#.#.#.#.#.#v#.#.#.#.###.#.#####.#.#v#.#.###.#.###.#.#.#.###v#.#.#.###.#.###.
#...#...>.>.#.#...#.#.#.#.#...#.#.#.#.#...#.#...#...#.#.#.#.#...#...#.#.#...###.#...#...#.#.#...
#########v###.###.#.#.#.#.#####.#.#.#.###.#.###.#.###.#.#.#.#.#####.#.#.#######.#######.#.#.#.##
#...#.....#...#...#.#.#.#...#...#...#.....#.#...#.#...#.#...#...#...#...###...#.....#...#.#.#.#.
#.#.#.#####.###.###.#.#.###.#.#############.#.###.#.###.#######.#.#########.#.#####.#.###.#.#.#.
#.#...#...#...#...#.#.#.#...#...#.........#.#...#...###...#...#...#.........#.....#.#.#...#.#.#.
#.#####.#.###.###.#.#.#.#.#####.#.#######.#.###.#########.#.#.#####.#############.#.#.#.###.#.#.
#.#.....#...#.....#.#.#.#.#...#...#...#...#.#...#...#...#...#.....#.............#...#.#...#.#.#.
#.#.#######.#######.#.#.#.#.#.#####.#.#.###.#.###.#.#.#.#########.#############.#####.###.#.#.##
#.#.#.......#...###...#...#.#.#.....#...###...###.#...#...........###.....#...#.....#...#.#.#.#.
#.#.#.#######.#.###########.#.#.#################.###################.###.#.#.#####.###.#.#.#.#.
#...#.........#.#.....#.....#...#...#.......#.....#.................#...#...#.......###...#.#.#.
###############.#.###.#.#########.#.#.#####.#.#####.###############.###.###################.#.##
#...............#...#.#...........#...#.....#.......#.............#.#...#.........###.....#...##
#.#################.#.#################.#############.###########.#.#.###.#######.###.###.######
#.#...............#.#.#...#...#.........#...#...#...#...........#...#.....#.......#...#...#...#.
#.#.#############.#.#.#.#.#.#.#.#########.#.#.#.#.#.###########.###########.#######.###.###.#.#.
#...#.............#.#.#.#...#.#.......#...#.#.#...#...#.........#.......###...#...#...#...#.#.#.
Day 24: Never tell me the odds
This day is the hardest day to test effectively. Due to the nature of the floating point calculations in most solutions, all of the tested solutions that didn't use some rational representation of numbers fail to reliably produce the correct solution. Double precision floats appear to not have enough accuracy to solve this 100% via LU or QR decomposition.
With that disclaimer out of the way, the actual generation process is pretty simple. We can observe that, if we were to translate the vectors of the hailstones into the reference frame of the thrown stone by subtracting the thrown stone's velocity, all of the hailstones intersect at the same point. We can use this to work backwards by:
- Generating a collision location for all of the hailstones.
- For 300 hailstones, generate a random velocity, ensuring velocities are unique and that we don't have velocities with zero dx, dy, or dz components.
- For each hailstone, pick a random time at which that stone will intersect the chosen point.
- Then, for each stone, determine a starting location using the chosen velocity and time such that it reaches the intersection point at that time.
- Pick a random velocity for the thrown stone and add that velocity to the velocity of every hailstone, again ensuring that we have no duplicated velocities or zero components.
Here's a portion of the generated output:
390208620113297, 387658594217963, 193982565362539 @ -159, -12, 52
355036790599893, 312445104395459, 168467997917289 @ -3, 316, 150
401732926148707, 373214493660286, 118299994706545 @ -145, 65, 142
420648511422477, 411386139859648, 169115406571609 @ -299, -121, 166
351790537980292, 393717989209348, 200452790602950 @ 120, -151, 131
385100857706287, 406584957673573, 258043531413369 @ -154, -164, -302
354198922055373, 344152181445027, 212788597527175 @ 13, 196, -32
411672501875421, 334321239163020, 241791789399506 @ -323, 295, -199
390963986881807, 372807703632133, 290029547517549 @ -139, 62, -301
325425038278699, 393861405431826, 308204209474103 @ 47, 7, -316
408904589305417, 382986915454783, 232364863629819 @ -332, -25, -145
372760882083647, 401414205535653, 279302686212777 @ -80, -36, -276
333378655149979, 292166485059259, 231162711493599 @ 9, 251, -105
326880735906259, 296630048460515, 252264371097802 @ 47, 276, -167
338657673735801, 368380469420643, 226344525861201 @ 166, 79, -102
389767366985692, 360210707727913, 250433420847429 @ -232, 158, -334
370953601893352, 311622495452713, 175998882578334 @ -72, 302, 103
273326204200381, 464924849593365, 149081033120033 @ 134, -134, 74
330595249803255, 338243685725309, 302133510130081 @ 31, 156, -296
399521852512378, 375535975955106, 236049883831312 @ -136, 61, -113
365976395159161, 345244743983209, 230932464609465 @ -22, 256, -138
348611106945922, 350922815557696, 282403269725901 @ -30, 113, -214
462518010517101, 269862968696667, 309025111805793 @ -311, 328, -306
434430584056654, 297012442141637, 266006011750730 @ -232, 250, -191
Day 25: Snowverload
The final day's input is simple enough to generate. The trick is hiding the fact that we generate the nodes in either half of the graph such that there exists no minimum cut smaller than 4 in either of them. This is done by only printing a subset of the edge relations if a particular edge was already covered by a different line in the input. We can randomly include or exclude duplicate edges this way.
- Generate two random graphs of 700-900 nodes where each node has at least four neighbors.
- Pick three nodes from each graph, grouping them so you have three pairs of nodes (one node from each graph in the pair).
- Join the pairs of nodes to form the bridge between the two graphs.
Here's a portion of the input:
xbd: vwx taq mzb
abz: kvz pau yyt taq kzi rsp
ctv: hjv lal
uls: mvp esd gpd qel epd
vuu: bbf lep ncy pmz bps qts vrt qzr
nvz: xkf vvb dub ypp xsd doe
xss: hmh lfj nyo guv nrs sep
mce: tmr laf ifq gcx zsm miu qyu boy yig xom
yog: elx wwz ied cst hee caz
the: tmh sqb
ifq: mce xsd cio yqd dlg qns pib
lly: kkt qzq oqe
hps: imj qix zhr ffc lqy ged
xgd: udu gpd
uhd: web zcb csk vzj won
kvz: ilx wig rpn
kpi: tiy sqb phe jgt hqa dax bqr
iym: rle fna prh hcw dpv
owf: rwj
mvp: uls deb lvt dax dgp ebz sck
gpn: drc idw mfz ymx
rtm: wkk ysu grv vaj
nnk: nit lac krv mva tmq
zij: jrp mws ivs
zvc: mqv ljl qwo hst
tgs: fvr dcp vrt ywi
Some closing thoughts.
While I wish there was an official way to get access to more inputs to test with, attempting to generate my own inputs has given me insights into problem construction and solution constraints that will likely aid me in future AoC years, as well as if I decide to create a answer-oriented challenge of my own at some point in the future.
In creating these inputs, I discovered bugs in my real solutions that I would have otherwise missed because of some artifact of the real input generation algorithms. My range splitting for day 19 was actually wrong, but passed for my input, and my day 24 accuracy isn't sufficient to solve all generated inputs. I suspect other people would benefit from these insights/inputs as well (if that was something they cared about).
Lastly, I can't guarantee my inputs will always be valid or that there aren't edge cases that I've missed, but I consider this a reasonable attempt at reverse engineering/approximating the input generation for most days this year.